37
— Возникает вопрос, — говорил пятый, — сколько форм существует у кубика, то есть форм настолько симметричных, что для каждых двух выбранных граней кубика его можно было повернуть таким образом, чтобы в новом положении он полностью совместился бы с самим собой, при этом первая из выбранных граней совместилась бы со второй. Таким образом все грани кубика оказались бы в определенном смысле равноправными, что служит залогом к тому, чтобы частота выпадения одной из них не опережала частоту выпадения другой. По моему мнению, именно это равноправие граней позволяет называть многогранник кубиком.
Перечисляя эти формы, во-первых назовем пять правильных многогранников: четырехгранник, шестигранник — уже нам знакомый, восьмигранник, двенадцатигранник и двадцатигранник. — Пятый раскрыл одну из своих тетрадей и показал рисунок.
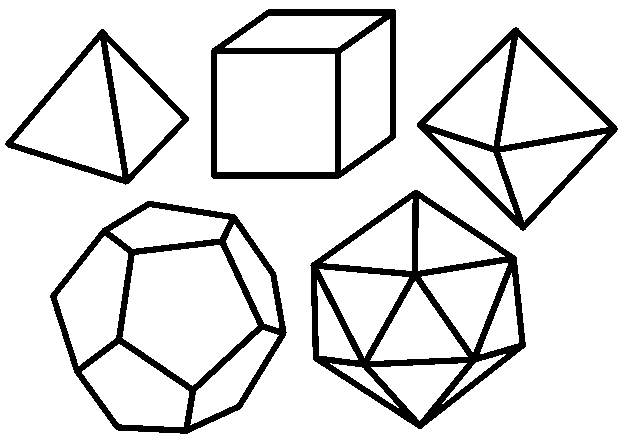
Во-вторых, это многогранники, образованные двумя одинаковыми пирамидами, которые совмещены основаниями, — продолжал пятый. — Таким способом могут быть получены кубики с любым четным числом граней, большим шести. Кстати, уже известный нам правильный восьмигранник может быть отнесен к этому типу.
Теперь, если у описанного только что многогранника мы слегка повернем составляющие его пирамидки одну относительно другой и определенным образом отрегулируем граничную линию между пирамидками, то получим кубик, составленный как бы из двух розеток. Его гранями уже будут не треугольники, как в предыдущем случае, а четырехугольники. Примером такого кубика является наш старый знакомый — шестигранный кубик, который можем разложить на две розетки, каждая из трех четырехугольников-квадратов.
Остальные формы кубиков можно получить из правильных многогранников. Для этого мы сперва каждую грань разбиваем на одинаковые и симметрично расположенные части — треугольники или четырехугольники. Это можно сделать, проводя из центра грани линии к ее углам (первый вариант) либо к серединам сторон (второй вариант). Третий вариант получится при совмещении первых двух.
Далее назначим центры граней исходного многогранника (а также середины его ребер в случае второго и третьего из рассмотренных вариантов) дополнительными вершинами нового кубика. Для придания телу этого кубика необходимой выпуклости приподнимем эти вершины над их первоначальным местом, представив, что ребра нового кубика (то есть проведенные нами линии, точнее — отрезки линий), которые сходятся в этих вершинах, потянутся, так сказать, за ними. Вершины исходного многогранника остаются, разумеется, на своем месте.
Замечу, что я рисовал простыми линиями и не клал штриховку на грани, поэтому на некоторых рисунках создается ощущение того, что выступающие вершины и ребра чередуются с утопленными, то есть получается как бы звездчатый многогранник. Иногда трудно избавиться от этого ощущения. Но на самом деле все многогранники выпуклые, это понятно.
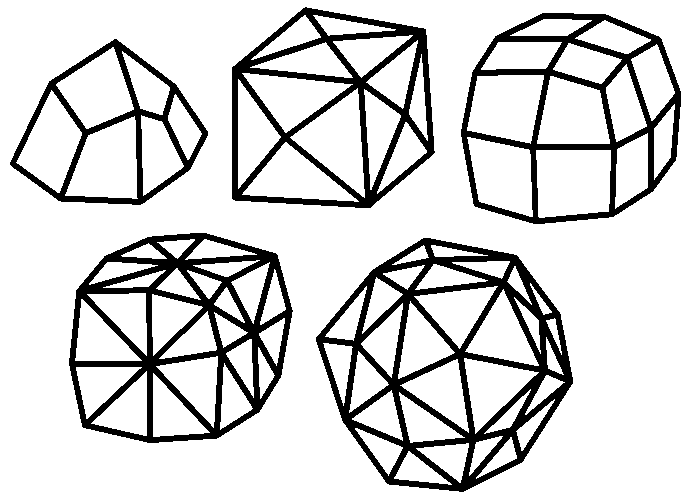
Проводя эти операции по трем возможным вариантам, мы получим:
- из четырехгранника — кубик с 12 треугольными гранями, кубик с 12 четырехугольными гранями и кубик с 24 треугольными гранями;
- из нашего знакомого шестигранника — кубик с 24 треугольными гранями, кубик с 24 четырехугольными гранями и кубик с 48 треугольными гранями;
- из восьмигранника — кубик с 24 треугольными гранями, кубик с 24 четырехугольными гранями и кубик с 48 треугольными гранями (при этом последние два кубика — это те же самые, которые были получены на основе шестигранника);
-из двенадцатигранника — кубик с 60 треугольными гранями, кубик с 60 четырехугольными гранями и кубик с 120 треугольными гранями;
- из двадцатигранника — кубик с 60 треугольными гранями, кубик с 60 четырехугольными гранями и кубик с 120 треугольными гранями (при этом последние два кубика — те же самые, которые были получены на основе двенадцатигранника).
Итого вместе с первоначальными пятью правильными многогранниками получается 16 кубиков различной формы (двойные пирамидки и двойные розетки, которые бесконечны числом, считать не будем). Однако один нерешенный вопрос меня беспокоит: исчерпывается ли число возможных типов кубиков этим числом 16, или же существуют другие, еще не найденные мной? И на этот вопрос у меня нет ответа.
Пятый замолчал, и все слушавшие с облегчением вздохнули.
